数据结构（十四）——二叉树

发布时间：2020-04-15 00:27:18 来源：51CTO 阅读：271801 作者：天山老妖S

数据结构（十四）——二叉树一、二叉树简介 1、二叉树简介

二叉树是由n（n>=0）个结点组成的有序集合，集合或者为空，或者是由一个根节点加上两棵分别称为左子树和右子树的、互不相交的二叉树组成。
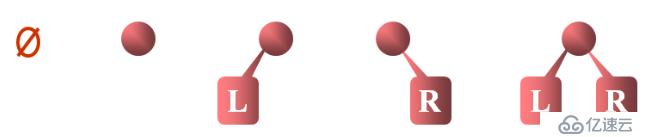
二叉树的五种形态：

数据结构（十四）——二叉树

2、二叉树的存储结构模型

树的另一种表示法：孩子兄弟表示法
A、每个结点都有一个指向其第一个孩子的指针
B、每个结点都有一个指向其第一个右兄弟的指针

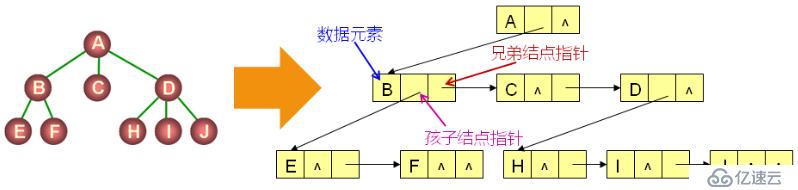
数据结构（十四）——二叉树

孩子兄弟表示法的特性：
A、能够表示任意的树形结构
B、每个结点包含一个数据成员和两个指针成员
C、孩子结点指针和兄弟结点指针构成树杈

3、满二叉树

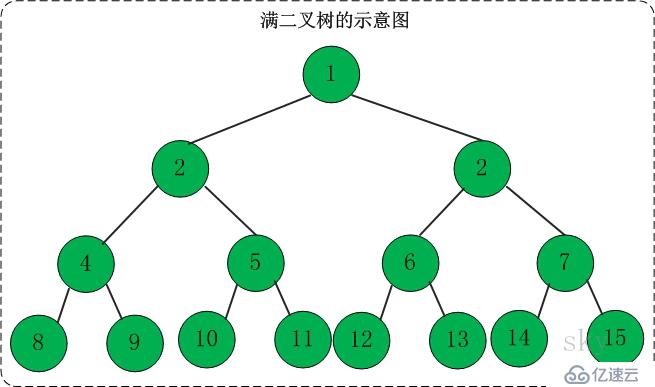
如果二叉树中所有分支结点的度数都为2，并且叶子结点都在统一层次上，则二叉树为满二叉树。

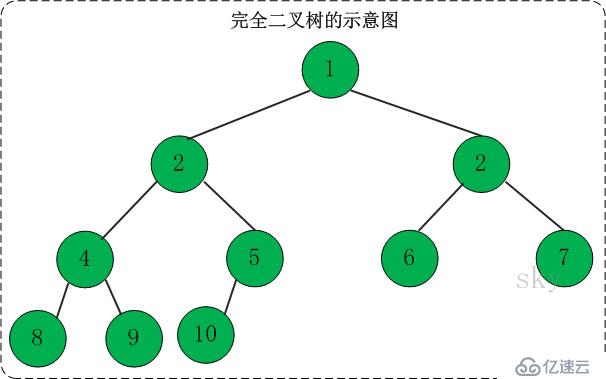
数据结构（十四）——二叉树

4、完全二叉树

如果一棵具有n个结点的高度为k的二叉树，树的每个结点都与高度为k的满二叉树中编号为1——n的结点一一对应，则二叉树为完全二叉树。
完全二叉树的特性：
A、同样结点数的二叉树，完全二叉树的高度最小
B、完全二叉树的叶子结点仅出现在最下边两层，并且最底层的叶子结点一定出现在左边，倒数第二层的叶子结点一定出现在右边。
C、完全二叉树中度为1的结点只有左孩子。

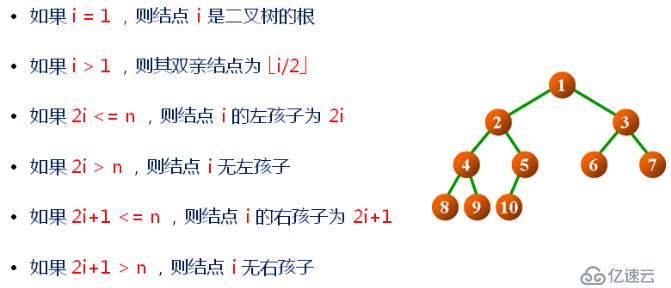
数据结构（十四）——二叉树

5、二叉树的特性

A、在二叉树的第i层上最多有2^(i-1)个结点（i>=1）。
B、高度为k的二叉树，最多有2^k-1个结点（k>=0）。
C、对任何一棵二叉树，如果其叶结点有n个，度为2的非叶子结点有m个，则
n = m + 1。
D、具有n个结点的完全二叉树的高度为logn + 1
E、对于有n个结点的完全二叉树，按层次对结点进行编号（从上到下，从左到右），对于任意编号为i的结点：

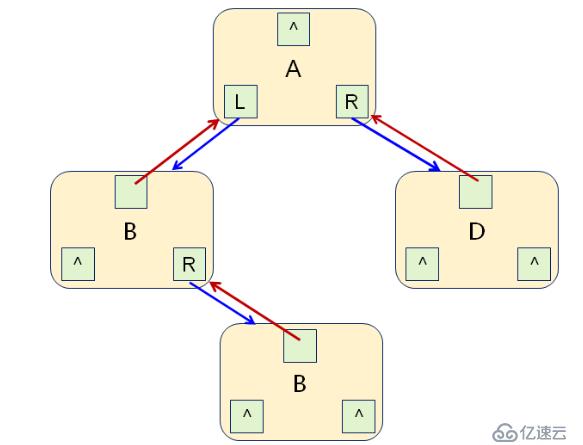
数据结构（十四）——二叉树

二、二叉树的操作 1、二叉树的存储结构实现

数据结构（十四）——二叉树

二叉树结点包含四个固定的成员：结点的数据域、指向父结点的指针域、指向左子结点的指针域、指向右子结点的指针域。结点的数据域、指向父结点的指针域从TreeNode模板类继承而来。
二叉树结点的实现：

template <typename T> class BTreeNode:public TreeNode<T> { public: BTreeNode<T>* m_left;//左子结点 BTreeNode<T>* m_right;//右子结点 BTreeNode() { m_left = NULL; m_right = NULL; } //工厂方法，创建堆空间的结点 static BTreeNode<T>* NewNode() { BTreeNode<T>* ret = new BTreeNode<T>(); if(ret != NULL) { //堆空间的结点标识为true ret->m_flag = true; } return ret; } }; 2、二叉树的结点查找

A、基于数据元素的查找
定义基于数据元素查找的函数

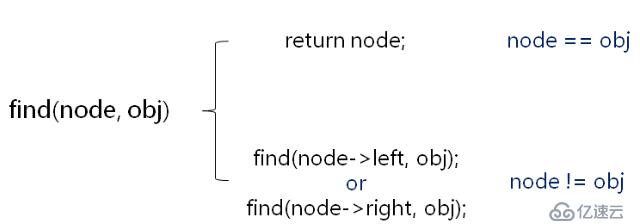
数据结构（十四）——二叉树

virtual BTreeNode<T>* find(BTreeNode<T>* node, const T& value)const { BTreeNode<T>* ret = NULL; //如果根节点node if(node != NULL) { if(node->value == value) { ret = node; } else { //查找左子树 if(ret == NULL) { ret = find(node->m_left, value); } //如果左子树没有找到，ret返回NULL，查找右子树 if(ret == NULL) { ret = find(node->m_right, value); } } } return ret; } BTreeNode<T>* find(const T& value)const { return find(root(), value); }

B、基于结点的查找
定义基于结点查找的函数

数据结构（十四）——二叉树

virtual BTreeNode<T>* find(BTreeNode<T>* node, BTreeNode<T>* obj)const { BTreeNode<T>* ret = NULL; if(node != NULL) { //根节点node为目标结点 if(node == obj) { ret = node; } else { //查找左子树 if(ret == NULL) { ret = find(node->m_left, obj); } //如果左子树没有找到，ret返回NULL，继续查找右子树 if(ret == NULL) { ret = find(node->m_right, obj); } } } return ret; } BTreeNode<T>* find(TreeNode<T>* node)const { return find(root(), dynamic_cast<BTreeNode<T>*>(node)); } 3、二叉树的结点插入

根据插入的位置定义二叉树结点的位置枚举类型：

enum BTNodePos { Any, Left, Right };

郑重声明：本文版权归原作者所有，转载文章仅为传播更多信息之目的，如作者信息标记有误，请第一时间联系我们修改或删除，多谢。